$\newcommand{\dede}[2]{\frac{\partial #1}{\partial #2} }
\newcommand{\dd}[2]{\frac{d #1}{d #2}}
\newcommand{\divby}[1]{\frac{1}{#1} }
\newcommand{\typing}[3][\Gamma]{#1 \vdash #2 : #3}
\newcommand{\xyz}[0]{(x,y,z)}
\newcommand{\xyzt}[0]{(x,y,z,t)}
\newcommand{\hams}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2} + \dede{^2}{y^2} + \dede{^2}{z^2}) + V\xyz}
\newcommand{\hamt}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2} + \dede{^2}{y^2} + \dede{^2}{z^2}) + V\xyzt}
\newcommand{\ham}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2}) + V(x)}
\newcommand{\konko}[2]{^{#1}\space_{#2}}
\newcommand{\kokon}[2]{_{#1}\space^{#2}} $
# Outline
| Thema | Notizen | Zeit |
| ----- | ------- | ---- |
| | | |
# Teile
## Motivation
Diese Woche habt ihr gelernt:
Strom, Kirchhof, Wiederstände.
## Recap Unterricht
### Repetition: Totales differential
Oft gesehen, dass durch dx geteilt wird. Don't do that... Nur Notation.
Was ist $df$
$df = \sum\limits_i\dede{f}{x_i}dx_i$
Wobei $dx_i$ ein "Einheitsvektor" ist. -> Division durch Vektoren sind nicht möglich.
Wenn ich jedoch einen Vektor umformen möchte, dann kann ich das via die obere Formel machen.
Wenn ich ein $df$ entfernen möchte, so muss ich die DGl lösen. (Bei 1D durch direkte Integration, bei mehreren Dim wie bei A3)
Was ist mit der Delta Methode? $x+dx$
Um dies korrekt zu machen müssen wir den Limes ausrechnen... -> Mühsam
### Was ist eine Kapazität?
Das verögen eines Bauteils bei einer gewissen Spannung eine gewisse Ladung zu halten.
Analogie:
Betrachte ein Rohrnetzwerk mit Wasser.
Q = Wassermenge
I = Fluss (Wasser/Zeit)
V = Druck
R = Reibung (Druck und Fluss stehen in einem Zusammenhang bei Rohren)
### Parallel und Serie schaltung von Kondensatoren
Motiviert am Beispiel des Plattenkondensators:
$C_{platte}= \frac{A\varepsilon_{0}}{{d}}$
### Feld/Ladung/Potential
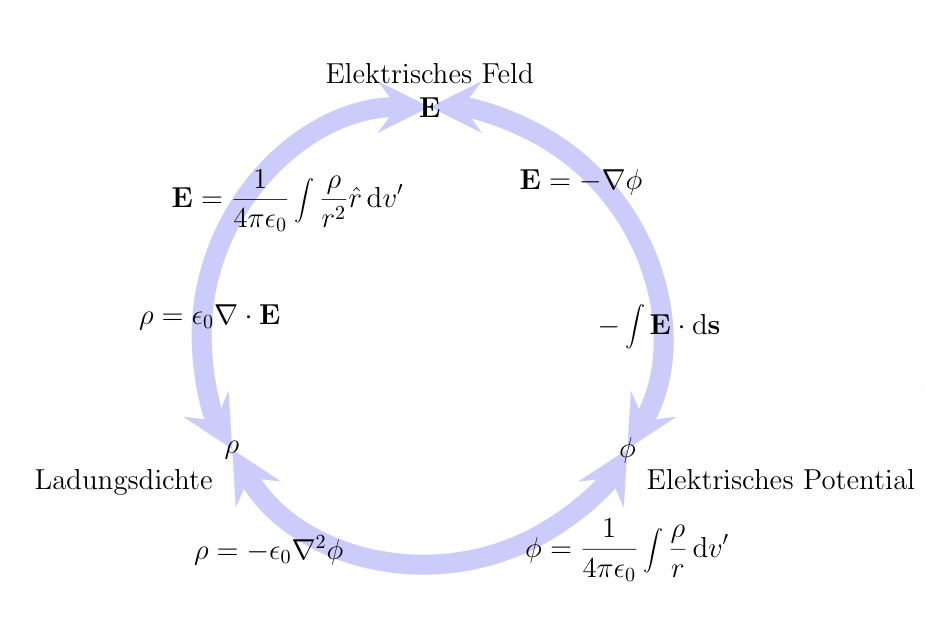### Strom
$I = \dd{Q}{t}$
### Stromdichte
$\vec J = n q v$
mit $I = J \cdot A$
### Driftgeschwindigkeit
(später relevant für relativität)
$n = \rho \frac{N_{A}}{M}$
$v = \frac{I}{neA}$
### Kontinuität
$\nabla \cdot J = -\dd{\rho}{t}$
Veränderung der Ladung pro Zeit ist die Divergenz (quellenstärke) der Stromdichte
### Ohm
$J = \sigma E = \rho^{-1} E$ mit $\rho$ der spezifische Wiederstand
$U=RI$
$R=\rho \frac{l}{A}$ : Breiterer Draht -> Weniger $R$ : Längerer Draht -> Mehr $R$
### Kirchhof
Die Kirchhofregeln:
1) $V=RI$
2) $\sum I = 0$ ;An jedem Punkt -> Entspricht Kontinuität
3) $\sum V = 0$ ;Für jede Schlaufe -> Entspricht Energieerhaltung
Tipps and Tricks:
1) Entferne redundante Bauteile
2) Simplifiziere via Ersatzschaltbild
3) Falls neu möglich gehe zu 1)
4) Stelle Sinnvolle Maschen auf.
5) Fülle auf mit Knoten bis genügend information
6) Maths.
7) Profit
### PUI
$P = \dot W = \dot Q V = IV$
### Batterie
Achtung! Innenwiederstand.
Eine Batterie ist keine ideale Spannungsquelle, dh. die tatsächliche Spannung ist lastabhängig.
Wir modelieren dies durch das hinzufügen eines kleinen Wiederstandes vor die Batterie. -> Limmitiert unseren Kurzschlusstrom
## MC
**a)** 3R
**b)** 4R
**c)** 7R
**d)** 5R
Welche Aussage ist korrekt?
**a)** Die Kontinuitätsgleichung folgt aus der Ladungserhaltung
**b)** = aus der Energieerhaltung
**c)** Die Spannung die über einen Wiederstand abfällt ist gleich der Leistung
**d)** Die Einheit der elektromotorischen Kraft ist $pa*m^2$
Welche Aussage ist korrekt?
**a)** Die maximale Spannung die eine Batterie erzeugen kann ist durch die interne chemische Reaktion (und nicht durch die Geometrie) begrenzt.
**b)** Eine 1.5V Batterie hat zwingend weniger Elektronen zur verfügung als eine 9V Batterie.
**c)** Bei Kondensatoren kann die Kontinuitätsgleichung nicht angewandt werden
**d)** Der Spannungsabfall über einen Kondensator ist proportional zu seiner Ladung
Frage: Wäre meine Unterrichtsvorbereitung Online eine Hilfe?
## Nachbesprechung Serie