$\newcommand{\dede}[2]{\frac{\partial #1}{\partial #2} }
\newcommand{\dd}[2]{\frac{d #1}{d #2}}
\newcommand{\divby}[1]{\frac{1}{#1} }
\newcommand{\typing}[3][\Gamma]{#1 \vdash #2 : #3}
\newcommand{\xyz}[0]{(x,y,z)}
\newcommand{\xyzt}[0]{(x,y,z,t)}
\newcommand{\hams}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2} + \dede{^2}{y^2} + \dede{^2}{z^2}) + V\xyz}
\newcommand{\hamt}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2} + \dede{^2}{y^2} + \dede{^2}{z^2}) + V\xyzt}
\newcommand{\ham}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2}) + V(x)}
\newcommand{\konko}[2]{^{#1}\space_{#2}}
\newcommand{\kokon}[2]{_{#1}\space^{#2}} $
# Outline
| Thema | Notizen | Zeit |
| ----- | ------- | ---- |
| | | |
# Teile
## Motivation
Grundlagen der Maxellgleichungen
Energie im Feld -> Kondensatoren
## Recap Unterricht
### Laplace Intuition und Anwendung:
$\Delta f= \dede{^2f}{x^{2}} + \ldots + \dede{^2f}{z^{2}}$
#### Laplace als Krümmung
In 1D entspricht Laplace genau der Krümmung. In mehr Dimensionen betrachten wir den Durchschnitt der Krümmungen
#### Laplace als Abweichung von der Umgebung
Entsprechend der Krümmungsanalogie sehen wir als konsequenz, dass wenn $\Delta f >0$ wir also im durchschnitt positiv gekrümmt sind, dann befindet sich der Mittelpunkt unterhalb des Durchschnitts (lokal)
#### Laplace als generalisierte Potentielle Energie
Wenn wir das Ursprüngliche Feld als eine Gespannte Oberfläche betrachten, dann entspricht der Laplace (mit noch ein paar faktoren) der Energie an diesem Punkt. (wie viel gespannter ist dieser Ort hier, als ein Anderer (in alle Richtungen im Schnitt))
#### Anwendung Wellengl
$$\frac{1}{c^{2}}\dede{^{2}f}{t} = \Delta f$$
Die Beschleunigung ist Proportional zum Unterschied zu den Nachbarn. (Je weiter die Nachbarpunkte unten sind, je schneller gleichen wir uns diesem An)
#### Anwendung Diffusion und Wärme
$\dede{u}{t} = \Delta u$
Die Geschwindigkeit ist proportional zum Unterschied zu den Nachbarn. Sind wir weit weg, so bewegen wir uns schnell. Sind wir jedoch nach, so werden wir abgebremst und nähern uns schlussendlich exponentiell an.
#### Anwendung Poisson Gleichung
$\Delta \varphi = \frac{\rho}{\varepsilon}$
Die Ladungsdichte ist proportional zum Unterschied meines Potentials zur Umgebung.
dh. Wenn ich mehr potential haben möchte als meine Umgebung, dann brauche ich Ladungsdichte. (ein Ort ohne Ladungsdichte kann nicht mehr Potential haben als der Durchschnitt der Nachbarn (im statischen fall))
#### Intuition Poisson Gleichung
$\Delta \phi = \frac{\rho}{\varepsilon} = 0$ überall wo keine Ladung ist.
Wir stellen uns ein Gespanntes Betttuch vor (wie oft in der Vorstellung der Gravitation). Wenn keine Masse bzw. Ladung vorhanden ist, so ist die Form vollständig durch den Rand gegeben (Wie eine Seifenblase). Wenn ich nun eine Kugel (masse bzw ladung) auf das Tuch lege, so gibt es lokal eine Delle (Proportional zur Masse). Die Neue Form des Tuches (entspricht dem Potential) Folgt nun der Poisson gleichung. (Überall wo keine Ladung ist, einfach nur gespannt, dort wo ladung ist gebogen proportional zur ladung.)
### Intensität
Energiedichte $\dd WV$
Mittlere Energiedichte $\langle \dd WV \rangle = \int$
Energieflussdichte $\bf{S} = \dd{^2W}{a dt}\hat n$
Intensität: $I=|S|$
$\sigma$ : Spannung
$E$: Elastizitätsmodul
__image couldn't be loaded__
#### Intensität
Betrachte nun die mittlere Energiedichte pro Periode
$$\langle \dd W V \rangle = \frac{1}{T}\int_{0}^{T}\dd W V dt$$
$$\langle \dd W V \rangle = \frac{1}{T}\int_{0}^{T}\rho v^{2}(\dede{f}{x})^{2}dt$$
für $f= A cos(kx -\omega t)$, $\dede f x = Ak\sin(kx-\omega t)$
$$\langle \dd W V \rangle= \frac{1}{T} \rho v^{2}k^{2}\int_{0}^{T}\sin^{2}(kx-\omega t)dt = \frac{1}{2}\rho v^{2}k^{2}A^{2}= \frac{1}{2} \rho \omega^{2}A^{2}$$
> Energie pro Volumen in einer Wellenperiode
Dieses Wellenpaket breitet sich aus mit der Phasengeschwindigkeit $v=\frac{\omega}{k}$ aus. (integral oben wegdenken)
Im Falle einer Ebenen Welle:
 ### Elektrostatik
#### Konventionen:
Energienullpunkt im unendlichen.
$F_{21}$ ist die kraft auf 2 von 1 (kommt von $r_{21} = r_{2}-r_{1}$)
#### Energie einer Ladungsverteilung
$W = \int_{\infty}^{d} -F_{21} ds = - \int_{\infty}^{d} \frac{1}{4\pi\varepsilon_{0}}\frac{q_{1}q_{2}}{r^{2}} = \frac{1}{4\pi\varepsilon_{0}}\frac{q_{1}q_{2}}{d}$
#### Das Elektrische Feld
$F = qE$
#### Ladungsverteilungen
Nimm Coulomb bei $x_0$ durch Ladung bei $x$
$E = \frac{1}{4\pi\varepsilon_{0}} \frac{Q}{|x_{0}-x|^{3}}(x_0-x)$
Copy-Paste dieses Feld überall dorthin wo wir ladungsdichte haben:
$E = \frac{1}{4\pi\varepsilon_{0}}\int_{\mathbb{R}^{3}}\frac{\rho(r’)}{|r-r’|^{3}}(r-r’)dx’dy’dz’$
#### Fluss
$d\Phi = E\cdot da$ “Anzahl Feldlinien pro fläche”
$\Phi = \int_{\partial V}E\cdot da$ “Alle Feldlinien”
#### Gauss
Anzahl neuer Feldlinien ist prop zu Ladungen
$\Phi = \frac{1}{4\pi\varepsilon_{0}}q \int_{\partial V} \frac{1}{r^{2}} = \frac{q}{\varepsilon_{0}}$
Generalisiert sich zu:
$\frac{1}{\varepsilon_{0}}\int_{V}\rho dV$
##### Gauss Example
Leiter mit linearer Ladungsdichte $\lambda$
#### Energie im Feld
Epsilon analog zu k bei Feder
## MC
### 1
### Elektrostatik
#### Konventionen:
Energienullpunkt im unendlichen.
$F_{21}$ ist die kraft auf 2 von 1 (kommt von $r_{21} = r_{2}-r_{1}$)
#### Energie einer Ladungsverteilung
$W = \int_{\infty}^{d} -F_{21} ds = - \int_{\infty}^{d} \frac{1}{4\pi\varepsilon_{0}}\frac{q_{1}q_{2}}{r^{2}} = \frac{1}{4\pi\varepsilon_{0}}\frac{q_{1}q_{2}}{d}$
#### Das Elektrische Feld
$F = qE$
#### Ladungsverteilungen
Nimm Coulomb bei $x_0$ durch Ladung bei $x$
$E = \frac{1}{4\pi\varepsilon_{0}} \frac{Q}{|x_{0}-x|^{3}}(x_0-x)$
Copy-Paste dieses Feld überall dorthin wo wir ladungsdichte haben:
$E = \frac{1}{4\pi\varepsilon_{0}}\int_{\mathbb{R}^{3}}\frac{\rho(r’)}{|r-r’|^{3}}(r-r’)dx’dy’dz’$
#### Fluss
$d\Phi = E\cdot da$ “Anzahl Feldlinien pro fläche”
$\Phi = \int_{\partial V}E\cdot da$ “Alle Feldlinien”
#### Gauss
Anzahl neuer Feldlinien ist prop zu Ladungen
$\Phi = \frac{1}{4\pi\varepsilon_{0}}q \int_{\partial V} \frac{1}{r^{2}} = \frac{q}{\varepsilon_{0}}$
Generalisiert sich zu:
$\frac{1}{\varepsilon_{0}}\int_{V}\rho dV$
##### Gauss Example
Leiter mit linearer Ladungsdichte $\lambda$
#### Energie im Feld
Epsilon analog zu k bei Feder
## MC
### 1
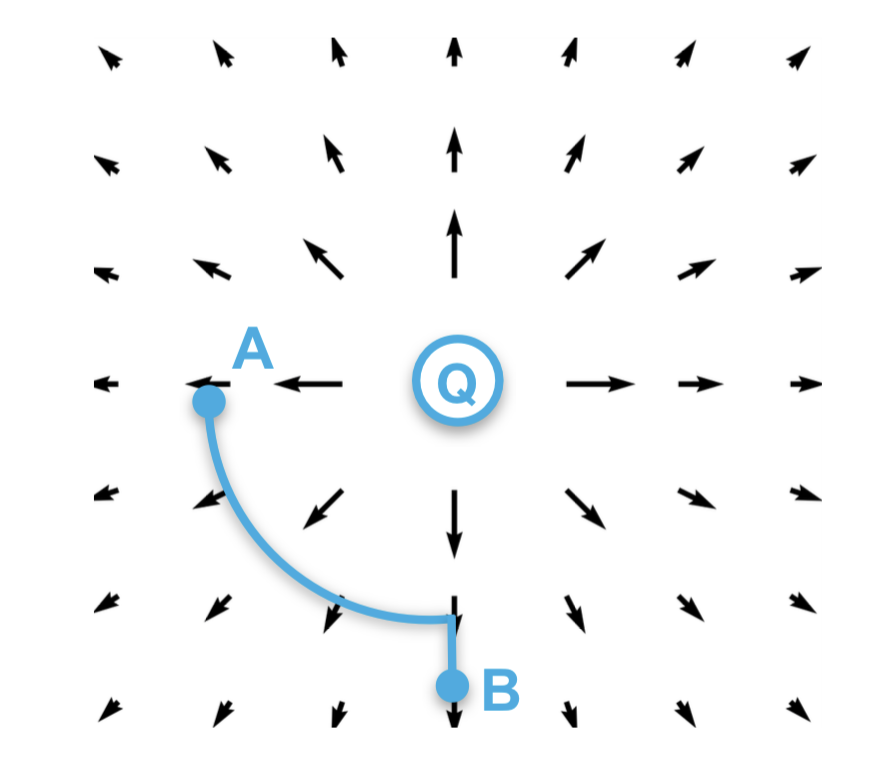 Es gilt:
**a)** Bei B ist das Potential grösser als bei A
**b)** Die Arbeit hängt davon ab welchen Weg wir nehmen
**c)** Ein Elektron hat eine höhere potentielle Energie bei B als bei A
**d)** Das gezeichnete Feld ist divergenzfrei
### 2
Für das Elektrische Feld gilt:
**a)** Überall wo keine Ladung ist gilt: $div(E) = 0$
**b)** Das Feld ist Konservativ gdw. $Q = 0$
**c)** Das Feld hat die Einheit Watt/Coulomb
**d)** Das Feld hat die Einheit eV
### 3
Eine Elektron sitzt bei 0, wir fügen ein Proton beim Abstand 10 A hinzu:
**a)** Die Beiden beginnen sich anzuziehen
**b)** Die Energie im Feld wurde verkleinert
**c)** Die Energie im Feld wurde vergrössert
**d)** Per Gauss ist $\rho = 0$ überall
## Nachbesprechung Serie
Es gilt:
**a)** Bei B ist das Potential grösser als bei A
**b)** Die Arbeit hängt davon ab welchen Weg wir nehmen
**c)** Ein Elektron hat eine höhere potentielle Energie bei B als bei A
**d)** Das gezeichnete Feld ist divergenzfrei
### 2
Für das Elektrische Feld gilt:
**a)** Überall wo keine Ladung ist gilt: $div(E) = 0$
**b)** Das Feld ist Konservativ gdw. $Q = 0$
**c)** Das Feld hat die Einheit Watt/Coulomb
**d)** Das Feld hat die Einheit eV
### 3
Eine Elektron sitzt bei 0, wir fügen ein Proton beim Abstand 10 A hinzu:
**a)** Die Beiden beginnen sich anzuziehen
**b)** Die Energie im Feld wurde verkleinert
**c)** Die Energie im Feld wurde vergrössert
**d)** Per Gauss ist $\rho = 0$ überall
## Nachbesprechung Serie
 Es gilt:
**a)** Bei B ist das Potential grösser als bei A
**b)** Die Arbeit hängt davon ab welchen Weg wir nehmen
**c)** Ein Elektron hat eine höhere potentielle Energie bei B als bei A
**d)** Das gezeichnete Feld ist divergenzfrei
### 2
Für das Elektrische Feld gilt:
**a)** Überall wo keine Ladung ist gilt: $div(E) = 0$
**b)** Das Feld ist Konservativ gdw. $Q = 0$
**c)** Das Feld hat die Einheit Watt/Coulomb
**d)** Das Feld hat die Einheit eV
### 3
Eine Elektron sitzt bei 0, wir fügen ein Proton beim Abstand 10 A hinzu:
**a)** Die Beiden beginnen sich anzuziehen
**b)** Die Energie im Feld wurde verkleinert
**c)** Die Energie im Feld wurde vergrössert
**d)** Per Gauss ist $\rho = 0$ überall
## Nachbesprechung Serie
Es gilt:
**a)** Bei B ist das Potential grösser als bei A
**b)** Die Arbeit hängt davon ab welchen Weg wir nehmen
**c)** Ein Elektron hat eine höhere potentielle Energie bei B als bei A
**d)** Das gezeichnete Feld ist divergenzfrei
### 2
Für das Elektrische Feld gilt:
**a)** Überall wo keine Ladung ist gilt: $div(E) = 0$
**b)** Das Feld ist Konservativ gdw. $Q = 0$
**c)** Das Feld hat die Einheit Watt/Coulomb
**d)** Das Feld hat die Einheit eV
### 3
Eine Elektron sitzt bei 0, wir fügen ein Proton beim Abstand 10 A hinzu:
**a)** Die Beiden beginnen sich anzuziehen
**b)** Die Energie im Feld wurde verkleinert
**c)** Die Energie im Feld wurde vergrössert
**d)** Per Gauss ist $\rho = 0$ überall
## Nachbesprechung Serie
 Es gilt:
**a)** Bei B ist das Potential grösser als bei A
**b)** Die Arbeit hängt davon ab welchen Weg wir nehmen
**c)** Ein Elektron hat eine höhere potentielle Energie bei B als bei A
**d)** Das gezeichnete Feld ist divergenzfrei
### 2
Für das Elektrische Feld gilt:
**a)** Überall wo keine Ladung ist gilt: $div(E) = 0$
**b)** Das Feld ist Konservativ gdw. $Q = 0$
**c)** Das Feld hat die Einheit Watt/Coulomb
**d)** Das Feld hat die Einheit eV
### 3
Eine Elektron sitzt bei 0, wir fügen ein Proton beim Abstand 10 A hinzu:
**a)** Die Beiden beginnen sich anzuziehen
**b)** Die Energie im Feld wurde verkleinert
**c)** Die Energie im Feld wurde vergrössert
**d)** Per Gauss ist $\rho = 0$ überall
## Nachbesprechung Serie
Es gilt:
**a)** Bei B ist das Potential grösser als bei A
**b)** Die Arbeit hängt davon ab welchen Weg wir nehmen
**c)** Ein Elektron hat eine höhere potentielle Energie bei B als bei A
**d)** Das gezeichnete Feld ist divergenzfrei
### 2
Für das Elektrische Feld gilt:
**a)** Überall wo keine Ladung ist gilt: $div(E) = 0$
**b)** Das Feld ist Konservativ gdw. $Q = 0$
**c)** Das Feld hat die Einheit Watt/Coulomb
**d)** Das Feld hat die Einheit eV
### 3
Eine Elektron sitzt bei 0, wir fügen ein Proton beim Abstand 10 A hinzu:
**a)** Die Beiden beginnen sich anzuziehen
**b)** Die Energie im Feld wurde verkleinert
**c)** Die Energie im Feld wurde vergrössert
**d)** Per Gauss ist $\rho = 0$ überall
## Nachbesprechung Serie