$\newcommand{\dede}[2]{\frac{\partial #1}{\partial #2} }
\newcommand{\dd}[2]{\frac{d #1}{d #2}}
\newcommand{\divby}[1]{\frac{1}{#1} }
\newcommand{\typing}[3][\Gamma]{#1 \vdash #2 : #3}
\newcommand{\xyz}[0]{(x,y,z)}
\newcommand{\xyzt}[0]{(x,y,z,t)}
\newcommand{\hams}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2} + \dede{^2}{y^2} + \dede{^2}{z^2}) + V\xyz}
\newcommand{\hamt}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2} + \dede{^2}{y^2} + \dede{^2}{z^2}) + V\xyzt}
\newcommand{\ham}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2}) + V(x)}
\newcommand{\konko}[2]{^{#1}\space_{#2}}
\newcommand{\kokon}[2]{_{#1}\space^{#2}} $
# Outline
| Thema | Notizen | Zeit |
| ----- | ------- | ---- |
| | | |
# Teile
## Motivation
Diese Woche habt ihr gelernt:
- Stehende Wellen:
- Tonhöhe von Instrumenten abschätzen
- Richtantennen arrays
- Wie man einen Laser verstärkt (optical resonnator)
- Warum Kugelwellen so nützlich sind
- Hyugens
- Beugung
- Die erste hälfte des bekannnten Doppelspaltexperiments
- Funktionsweise vieler Spektrometer (Wichtig als Grundlage vieler experimente)
- Warum man um die Ecke hören kann
- Optik
- Wie das Internet so schnell ist (Glasfasern)
- Doppler
- Eine Methode zur Abschätzung wie schnell Boote fahren
- Warum die Frequenz der Ambulanz sich ändert beim vorbeifahren
## Recap Unterricht
### Stehende Welle
Betrachte 2 Wellen: $$\cos(kx - \omega t) + \cos(-kx -\omega t + \delta_R) = 2A\cos(kx)\cos(\omega t)$$ (mithilfe $\cos(a)\cos(b) = \frac{\cos(a+b)+\cos(a-b)}{2}$)
Bemerke, dass wir jetzt Zeit und Raum komponenten getrennt haben, welches qualitative verhalten erwarten wir?
#### Hartes vs Weiches Ende:
Wie wir bereits aus der normalen Reflektion gesehen haben, gibt es zwei qualitativ unterschiedliche Lösungen für die Reflektion:
1) Reflektion am harten Ende: Phasensprung, da nicht “die gesamte Amplidtude im neuen Medium Platz hat”
2) Reflektion am weichen Ende: Kein Phasensprung
Beispiele dafür sind:
1) Saiten
2) Blasinstrumente
 #### Energietransport
Wenn die Welle mal aufgebaut ist sehen wir (durch die Trennung der Orts/Zeitkomponenten), dass wir eigentlich für jeden Ort einen eigenen harmonischen Oszilator haben.
Wir sehen das Resultat auch, wenn wir die Energieverteilung explizit berechnen (1.172)
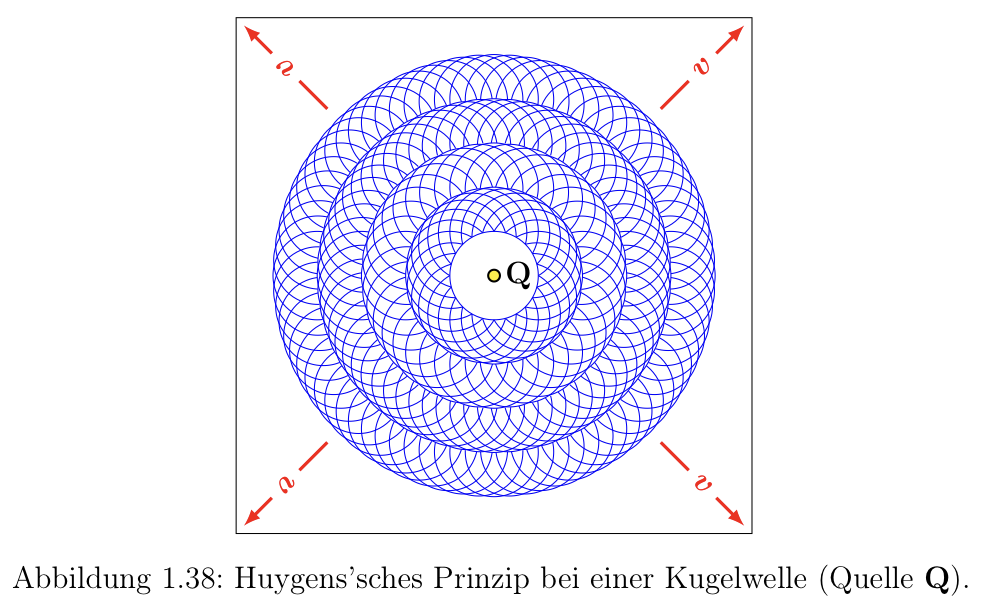
### Huygensches’ Prinzip
Jeder Punkt emmitiert eine Kugelwelle, welche in der Überlagerung/Superposition zur beobachteten Welle führen.
Wellenfläche: $k\cdot r - \omega t = \delta$
#### Energietransport
Wenn die Welle mal aufgebaut ist sehen wir (durch die Trennung der Orts/Zeitkomponenten), dass wir eigentlich für jeden Ort einen eigenen harmonischen Oszilator haben.
Wir sehen das Resultat auch, wenn wir die Energieverteilung explizit berechnen (1.172)
### Huygensches’ Prinzip
Jeder Punkt emmitiert eine Kugelwelle, welche in der Überlagerung/Superposition zur beobachteten Welle führen.
Wellenfläche: $k\cdot r - \omega t = \delta$

 #### Doppelspalt mit Huygens
#### Doppelspalt mit Huygens
 ## MC
> Welche Aussagen sind korrekt?
- Das Huygen’sche Prinzip besagt, dass die Flächen gleicher Phase immer eine Kugel bilden
- Bei der Stehenden Welle wird die Energie immer zwischen den “Bergen” und “Tälern” hin und her transportiert
- Beugung und Brechung sind das selbe Phänomen
- Totalreflektion gibt es nur beim Übergang von einem dichten in ein weniger dichtes medium
> Auf einem Zug steht ein Saxophonspieler, er spielt einen ein C. Welche Aussagen sind korrekt
- Beim Vorbeifahren erklingt der ton zuerst tief, dann hoch
- Beim Vorbeifahren erklingt der ton zuerst hoch, dann tief
- Ob der Zug an mir vorbeifährt, oder ob ich am Zug vorbeifahre spielt keine Rolle
- Wenn der Zug im perfekten Kreis um mich fahren würde, gäbe es keinen Doppereffekt
> Bei einer Beugung am Spalt ist die Reihenfolge der Farben, von innen nach aussen:
- Weiss, Blau, Gelb, Rot
- Rot, Gelb, Blau, Weiss
- Blau, Gelb, Rot
- Rot, Gelb, Blau
## Nachbesprechung Serie
### A4 Polarisation
$$\vec n = cos \theta \vec e_{x}+ sin \theta \vec e_{y}= \begin{pmatrix} cos \theta \\ sin \theta \\ 0 \end{pmatrix}$$
Ist linear, da $\vec n$ sich nicht ändert.
### A5 Gedämpfter Oszillator
**a)** Wirkende Kräfte: $$F_{tot} = F_{feder}+F_{reibung} = -D\vec x -6\pi \eta r \vec v$$
$F=ma = m \ddot x$
$$\ddot x = \frac{-D}{m}x - \frac{6\pi \eta r \dot x }{m}$$
$$\ddot x + 2(\frac{3\pi\eta r}{m} )\dot x + \sqrt{\frac{D}{m}}^{2}x =0 $$
$$\gamma = \frac{3\pi \eta r}{m}$$
$$\omega_{0}= \sqrt{\frac{D}{m}}$$
## MC
> Welche Aussagen sind korrekt?
- Das Huygen’sche Prinzip besagt, dass die Flächen gleicher Phase immer eine Kugel bilden
- Bei der Stehenden Welle wird die Energie immer zwischen den “Bergen” und “Tälern” hin und her transportiert
- Beugung und Brechung sind das selbe Phänomen
- Totalreflektion gibt es nur beim Übergang von einem dichten in ein weniger dichtes medium
> Auf einem Zug steht ein Saxophonspieler, er spielt einen ein C. Welche Aussagen sind korrekt
- Beim Vorbeifahren erklingt der ton zuerst tief, dann hoch
- Beim Vorbeifahren erklingt der ton zuerst hoch, dann tief
- Ob der Zug an mir vorbeifährt, oder ob ich am Zug vorbeifahre spielt keine Rolle
- Wenn der Zug im perfekten Kreis um mich fahren würde, gäbe es keinen Doppereffekt
> Bei einer Beugung am Spalt ist die Reihenfolge der Farben, von innen nach aussen:
- Weiss, Blau, Gelb, Rot
- Rot, Gelb, Blau, Weiss
- Blau, Gelb, Rot
- Rot, Gelb, Blau
## Nachbesprechung Serie
### A4 Polarisation
$$\vec n = cos \theta \vec e_{x}+ sin \theta \vec e_{y}= \begin{pmatrix} cos \theta \\ sin \theta \\ 0 \end{pmatrix}$$
Ist linear, da $\vec n$ sich nicht ändert.
### A5 Gedämpfter Oszillator
**a)** Wirkende Kräfte: $$F_{tot} = F_{feder}+F_{reibung} = -D\vec x -6\pi \eta r \vec v$$
$F=ma = m \ddot x$
$$\ddot x = \frac{-D}{m}x - \frac{6\pi \eta r \dot x }{m}$$
$$\ddot x + 2(\frac{3\pi\eta r}{m} )\dot x + \sqrt{\frac{D}{m}}^{2}x =0 $$
$$\gamma = \frac{3\pi \eta r}{m}$$
$$\omega_{0}= \sqrt{\frac{D}{m}}$$

 #### Doppelspalt mit Huygens
#### Doppelspalt mit Huygens

 #### Doppelspalt mit Huygens
#### Doppelspalt mit Huygens